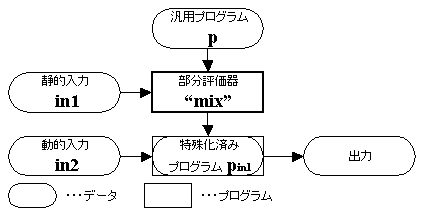
図 1 部分評価器
部分評価の紹介
An Introduction to Partial Evaluation (Neil D. Jones, ACM Computing Survey Vol.28 No.3 Sep. 1996)
部分評価器(partial evaluator)は、ある汎用プログラムから特定の入力に特化したプログラムを生成するプログラム特殊化器(program specializer)とみなせる。
図 1はプログラムpとpへの入力データの一部in1を取ってプログラムpin1を生成する部分評価器「mix」の模式図。ここでプログラムpin1はpに対する残りの入力in2を取ってpが入力in1、in2を取った場合と同一の出力を返すプログラム。

図 1 部分評価器
(の例で):
[[p]]
[in1, in2] = [[pin1]] [in2]
この記法ではin2に関する停止性についても両辺が等しいことが表される
[[p]]S[in1, in2] = [[ [[amix]]L[p, ] ]]T in2
のようにプログラムを表す[[ ]]に添え字をつけてそのプログラムの記述言語を明示することもある(この例のamixでは関数型言語を入力してスタック・マシンのコードを出力する[Holst 1988])。上記の添え字の意味はそれぞれ
S:
ソース言語
L: 実装言語
T: 目的言語
部分評価の第1の目的は高速化。
あまり変更されない部分が評価できれば、何度も走らせた場合に高速化が達成できる。
tmix(p, in1) + tpin1(in2) < tp(in1, in2)
(1度だけ実行する場合に高速化できるための時間的な条件)
利用される技法
1. 記号計算(symbolic computation)
2. 展開(unfolding)
3.
プログラム・ポイント特殊化(program point specialization)
以下2つをあわせてメモライゼーション(memorization・・・関数値を覚えておく)の効果。
(ア) 定義生成(definition creation)
(イ) 畳み込み(folding)

図 2:xn計算の特殊化
図 2の事例:
l
記号計算と展開の技法のみを利用している。
(これらによって特殊化したプログラムに関数呼び出しが含まれないからプログラム・ポイント特殊化は不要。)
l この事例ではプログラムの制御に無関係なxを特殊化しても高速化には繋がらない。
図 3の事例:
l プログラム・ポイント特殊化も利用。
l 実用的ではないがプログラム・ポイント特殊化のよい例。
オフライン特殊化(offline
specialization):
まずソースに(残留部(residual)を指定する)annotationを追加→annotationを特殊化器が解釈して特殊化
オンライン特殊化(online
specialization):
2段階に分けずに特殊化を行う。特殊化の過程でわかった情報でさらなる特殊化が可能ならばそれを実行する。
長所:
l
出来上がるコードの速度効率は一般に向上する。
例:a1(n)とa2(n)のif文でテストが真の場合については定数まで計算が進められる。
短所:
l 特殊化に掛かる時間は増加する。
l 特殊化が停止しないかもしれないという問題を持つ。
以下のような形式で一階の関数型言語で書かれたプログラムについて考える:
f1(s,d) =
expression1
g(u, v, ・・・) = expression2
・・・
h(u, v, ・・・) = expressionm
以下の2つの部分に分けて印をつける:
l 除去可能部(eliminable): 特殊化を通じて計算されたり展開されたりする部分。
l 残留部(residual): 特殊化された後も残る部分。
特に全ての関数定義について引数を以下の2つに分ける:
l 静的(static)
l 動的(dynamic)
特殊化されたプログラムは元のプログラムと同一の形式をもつが、(g, Statvalues)の各対に対応する特殊化済関数(specialized functions プログラム・ポイント(program point))gstatvaluesの定義を含む。
このアルゴリズムの出力は関数定義の集合Target
(プログラムにはannotationがつけられているものとする。)
1. プログラムProgramと静的入力Sを読み込む。
2.
初期化:
処理中の関数の集合 Pending{f1s};
処理済関数の集合 Seenbefore{};
3. 集合Pendingが空になるまで4〜6を繰り返す。
4. Pendingから対gstatvaluesを選び(もしまだ追加されていなければ)集合Seenbeforeに追加する。
5.
関数gの定義
g(x1, x2, ・・・) = g-expression
を見つけその動的な引数をD1, ・・・, Dmとする。
6.
関数定義
gStatvalues
(D1, ・・・ , Dm) = Reduce(E)
を生成してTargetへ追加する。
(ここで式Eはg-expression中の静的引数であるxiをStatvaluesに含まれるSiで置換したもの。)
1. 式Eが関数の動的パラメータならば、RE = E
2. 式Eが関数の静的パラメータならば、RE = (Statvaluesから取り出したその式の値)
3. Eが演算子operator(E1,・・・ ,En)の形式ならばEiの値vi=Reduce(Ei)を計算(これが計算できないときはannotationが誤り)し、RE = operator(v1,・・・ ,vn)・・・値になる。
4. Eが演算子operator(E1,・・・ ,En)の形式ならばEi' =Reduce(Ei)を計算して、RE =operator(E1',・・・ ,En')・・・式になる。
5. Eが演算子if E0 then E1 else E2の形式ならばE0の真偽値Reduce(E0)を計算(これが真偽のどちらかとして計算できないときはannotationが誤り)し、真ならばRE = Reduce(E1)偽ならばRE = Reduce(E2)
6. Eが演算子if E0 then E1 else E2の形式ならばEi' =Reduce(Ei)を計算して、RE = if E0' then E1' else E2'・・・式
7.
Eが関数f(E1,・・・ ,En)の形式であれば、RE
= Reduce(E')。
E'はプログラム中にあるf(x1, ・・・ , xn)=f-expressionという定義について、f-expression中の静的な引数xiをReduce(Ei)に置換したもの
8. Eが演算子f(E1,・・・ ,En)の形式ならば
(a) 関数fの各引数についてReduceを呼び出して関数fの静的引数Statvalues'(引数と定数値の組のリスト)を求める。(これが計算できないときはannotationが誤り)
(b) 関数fの各引数についてReduceを呼び出して関数fの動的引数Dynvalues(式のリストになる)を求める。
(c) 関数呼び出しを結果として返す。
RE = fStatvalues'(Dynvalues)
(d) 副作用: 関数fStatvalues'がPendingにもSeenbeforeにも含まれていなければ、Pendingに追加する
合同条件(congruence
condition): プログラムの適切な部分がannotateされる。
最低限、削除可能とマークされた全ての引数と演算については、ありえる全ての静的な入力について特殊化できることが保証されること。
終了条件(termination condition): 静的な入力の値に関わらず特殊化が終了すること(無限に沢山の関数や式が出力されない)。
束縛時解析(binding time analysis)では、これらの条件を満足するようにannotationする必要がある。
現状の技術では、合同条件は完全に自動的に満たせるが、終了条件の保証に関しては端緒についたばかり(1966年時)。
一段階計算による解法ととプログラム生成を利用した多段階解法の比較
例:
コンパイラ: ソース言語で書かれたソース・プログラムからターゲット言語で書かれたターゲット・プログラムを生成。ターゲット・プログラムの実行効率が命。
パーサ・ジェネレータ: 文脈自由文法からそれで定義される言語のパーサを生成。
どちらも文字列入力を実行可能プログラムに変換する。そのプログラムを実行すると前者ではコンパイルを行い後者では構文が解析される。
図 4はコンパイラを利用した2段階の実行とインタプリタによる2段階の実行の比較。
図 4:コンパイラは2段、インタプリタは1段
補足表 1: インタプリタとコンパイラの得失
|
|
インタプリタ |
コンパイラ |
|
作成 |
小さく簡単 (一個の言語に対する動作を一度だけ考えればよい) |
大きく難しい (ソース言語での動作と生成されたターゲット言語での動作の双方を考えねばならない) |
|
言語定義 |
高級言語で直接に操作的意味付けをしながら定義できる |
|
|
効率 |
実行毎に解釈のオーバーヘッド |
一般にコンパイル済みのコードは高速に実行可。 2フェーズならば1フェーズ目で大局的な情報を利用して2フェーズ目のプログラム最適化が可能 (例: コンパイラの型チェックとかパーサ・ジェネレータの文法クラス・チェックとか) |
|
等式表記 |
[[src]]S d = [[interpreter]]L [src, d] |
[[src]]S d = [[ [[compiler]]L src]]T d |
アイディア:
固定されたソースの入力に対してインタプリタを特殊化する。
target = [[mix]] [interpreter, src]
(ここでmixはソースに加えてinterpreterという静的入力も必要なのでコンパイラではない。)
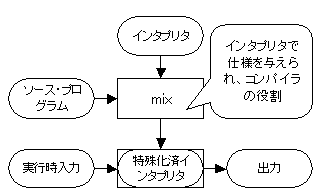
補足図 1:
特定のソースに対するインタプリタの特殊化
l
ソース言語: 7命令の命令型言語
X:=X+1, X:=X-1,
Y:=Y+1, Y:=Y-1,
(IFY=0GOTO label), (IFX=0GOTO label),
(GOTO label)
l 実装言語: 簡単な関数型言語

図 5: 命令型言語のために関数型言語で記述されたインタプリタ
操作的意味論付きの言語定義について部分評価ならば:
l 解釈時のオーバーヘッドを削減できる。
l
インタプリタで通るソースからのターゲット・プログラムはいつも正しい。(mixが正しいと仮定した場合)
→ コンパイラの正しさの問題は解消
→ 新言語のプロトタイプの実装に向いている
(関数型言語では初期から行われていた。)。
l
一般に部分計算の出力はインタプリタの実装言語
→きちんとしたソース言語からターゲット言語を作り上げる(PascalからP-codeのように)ものではない。
l
新たな実行時データ構造の発明を意図したものではないので、完全に手で書かれたコンパイラの効率を得るためにはまだまだ人の創造性が必要。
(しかし、近年の研究[Hannan
and Miller 1990]でターゲット・マシンのアーキテクチャからインタプリタのコードを導ける可能性が提案された。)
l
部分計算系は自動的かつ汎用的なので手書きのターゲット・コードには及ばない。特に今のところ中間言語やハードウェアに依存する古典的な最適化技法(例:
共通部分式の除去、レジスタ割り当て)については考慮に入れられていない。
(将来はこれらの技法を取り入れた次世代の部分評価器が現れるかも・・・。)
(構文解析→部分式の評価)を再帰呼び出しによって繰り返し、主だった演算子(算術演算や変数参照)にぶつかると演算が実行される。
ap・tp(d) ≦ tint(p, d)
l apはdには独立だがpに依存する定数。
l 経験的には単純なインタプリタでは約10。
l (データ構造にhash表や2分木を利用するような)洗練されたインタプリタではpが増加しても増え方が小さい傾向がある。
最良の実装をされたmixはインタープリテーションのオーバーヘッドを全て取り除けるべき。
詳細:
言語Lで書かれた言語Lのインタプリタ(セルフ・インタプリタ(self-interpreter))sintを考える。
理想的なmixはsintの実行に対するapを1にできねばならない。
任意のプログラムpと入力dについて
[[p]] d = [[sint]] [p, d]
= [[
[[mix]] [sint, p] ]] d
だからp' = [[mix]] [sint. p]はプログラムpと等価。
もしp'が少なくともp程度には効率的ならば、解釈時のオーバーヘッドは取り除かれている筈。
mixの最良性の定義:
任意のp、dについて
tp'(d) ≦ tp(d)
であること。ここでp' = [[mix]] [sint. p]、sintはセルフ・インタプリタ
現状:
この最良性の規準は幾つかの部分計算系では様々な言語のセルフ・インタプリタについて満たされている。(それぞれ各p'はpと変数の名前と順序を除いて同一。)
先に述べた実行速度の向上はこの性質から説明できる。
図 6はLisp類似の関数型言語で書かれた正規表現認識器。これを正規表現(a+b)*abbについて特殊化したものが図 7。
正規表現の文法:
regexp
::= symbol | () | (regexp *) | (regexp + regexp) | (regexp regexp)
正規表現認識器のコード(Lisp状表現):
(define (rex r s)
(case s of
() : (accept-empty? r)
(symbol . srest) : (rex1 r symbol srest (firstcharacters r))))
(define (rex1 r0 symbol srest firstchars)
(case firstchars of
() : #f
(f . frest) : (if (equal? symbol f)
then (rex (next r0 f) srest)
else (rex1 r0 symbol srest frest))))
(define (accept-empty? r0)
(case r0 of
() : #t
(r1 *) : #t
(r1 + r2) : (or (accept-empty? r1) (accept-empty? r2))
(r1 r2) : (and (accept-empty? r1) (accept-empty? r2))
else : #f))
(define (next r0 f) ... )
(define firstcharacters r0) ... )
図 6: 正規表現認識器
l 正規表現認識器は文字列を入力し、それが正規表現(例: (a+b)*abb)であれば真#t、そうでなければ偽#fを返す。
(define rex-0 s)
(case s of
() : #f
(s1.sr) : (case s1 of 'a: (rex-1 sr) 'b: (rex-0 sr) else #f)
(define (rex-1 s)
(case s of
() : #f
(s1.sr) :
(case s1 of
'a : (rex-1 sr)
'b : (case sr of
() : #f
(s2.sr2) : (case s2 of
'a : (rex-1 sr2)
'b : (case sr2 of
() : #f
(s3.sr3) : (case s3 of
'a : (rex-1 sr3)
'b : (rex-0 sr3)
else : #f))
else : #f))
else : #f)))
図 7: r = (a+b)*abb用に特殊化された正規表現認識器
l rexを「コンパイル」すれば字句解析器が得られる。これはrexをインタプリタ、正規表現をソース、と考えて特殊化していることになる。
l 特殊化によって出来上がったプログラムは与えられた正規表現(例えば(a+b)*abb)を受理する有限オートマタになっている。(部分評価器は有限オートマタについて何も知らないで単に特殊化しているだけであるのに)
部分計算によって特殊化された版を高速に生成するために部分計算を利用できないか?
束縛時エンジニアリング(Binding-time engineering)
図 8のようにプログラム・ジェネレータの生成によって行われる。
(1) pin1は高速化されるはず。
(高速なターゲット・プログラム)
(2) p-genは高速にpin1を作成できるはず。
(高速なコンパイラ)
(3) cogenは高速にp-genを作成できるはず。
(高速なコンパイラ生成)
目標は完全に自動的な方法により高速なプログラム・ジェネレータを作成すること。
汎用プログラムは全体として、プログラム・ジェネレータが生成した特殊版より簡単になるが効率は劣る。

図 8: プログラム・ジェネレータの生成
特化されたプログラムと比べて経験上遅すぎるために極端に一般的なプログラムは(プログラムの実行やパースのために)滅多に利用されない。
例: specification executers
実行可能仕様の直接性や簡潔さと、プログラムジェネレータにより生成されたプログラムの効率性を両立したい
→ プログラム・ジェネレータのジェネレータ(図 8)
¨ プログラムcogenは2入力のプログラムを受け取ってプログラム・ジェネレータp-genを生成
¨ プログラムp-genは与えられた静的入力in1を受け取って特殊化されたプログラムPin1を生成
¨ プログラムpin1はpの残りの入力in2を受け取ってとp同じ結果を出力
これがGenerating Extension[Ershov 1982]で部分計算によって理論的にも実用的にも実現された。
図 2の例をこの手法で記述したものが図 9。(出力コードは一重引用符と結合演算子++で非形式的に記述)

図 9: 冪乗xn計算のためのGenerating Extension
mixについて以下の等式が成り立つ。
out = [[src]]S inp
= [[int]] [src, inp]
= [[ [[ mix]] [int, src] ]] inp
= [[tgt]] inp
以上より
tgt = [[mix]] [int, src]・・・第1二村Projection
tgtの記述言語は基本的にインタプリタの記述言語と同じ。
インタプリタを特定のソースに特化して(生のインタプリタより高速な)目的プログラムを生成することはコンパイラの働きに類似すると考える。
第1よりmixについて以下の等式が成り立つ。
tgt = [[mix]] [int, src]
= [[ [[mix]] [mix, int] ]] src
= [[comp]] src
以上より
comp = [[mix]] [mix, int]・・・第2二村Projection
コンパイラの記述言語は基本的にmixの記述言語と同じ。
mixを特定のインタプリタに特化してできたものは、ソースから(第1二村Projectionの意味で)目的プログラムを生成するから(生のソースにインタプリタを特化させたものより高速な変換を行う)コンパイラ。
mixについて以下の等式が成り立つ。
[[p]] [in1, in2] =
[[ [[mix]] [p, in1] ]] in2 =
[[ [[ [[ [[mix]] [mix, mix] ]] p ]] in1]] in2 =
[[ [[ [[cogen]] p]] in1]] in2
以上より
cogen = [[mix]] [mix, mix]・・・第3二村Projection
コンパイラ・ジェネレータの記述言語は基本的にmixの記述言語と同じ。
mixをmixに特化してできたものは、インタプリタから(第1二村Projectionの意味で動作する)コンパイラを生成するから(生のmixにインタプリタを特化させるより高速な変換を行う)コンパイラ生成器。
以上よりプログラム生成の各スタイルには2通りの方法がある。
tgt = [[mix]] [int, src]
= [[comp]] src
comp = [[mix]] [mix, int]
= [[cogen]] int
cogen = [[mix]] [mix, mix]
= [[cogen]] mix
mixやintの設計、実装言語Lの選択によって色々あるが、何人かの研究者によって各ケースで2つ目の方法が1つ目の10倍程度早いことが観察されている。
(実行にはmixを直接使うよりはコンパイラを作ったほうが早く、
コンパイルにはmixを直接使うよりはコンパイラ・ジェネレータでコンパイラを作ったほうが早く、
コンパイルの生成にはmixを直接使うよりはコンパイラ・ジェネレータでコンパイラ・ジェネレータを作ったほうが早い。)
→事実上はSelf-applicationする方が10倍早い
intとして実装言語自身のインタプリタを指定するとcompilerはLからLへの変換プログラムになる。
→インタプリタの実装方法を変更してプログラミング・スタイルの変換に利用できる。
例:
(1) サブセットへ
(2) 自動instrumentation(ステップ・カウント、トレースの表示、デバッグ情報の表示)[Bondorf 1991]
(3) 直接的なスタイルをcontinuation-passingスタイルへ
(4) lazyプログラムをeagerプログラムへ[Jorgensen 1992]
(5) 直接的なスタイルを末尾再帰スタイルへ(Binding-time separationはかなり難しい)[Sperber and Thiemann 1996]]
エキスパートシステムにおける幅広い要求を表現するためにユーザー志向言語が工夫されてきたが、それらの言語は幾つかのインタプリタ言語で階層的に実装されていて、そのオーバーヘッドが問題になってきた。
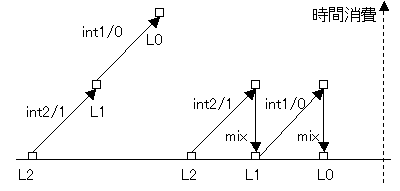
図 10: オーバーヘッドの発生と削減
L2でL1が、L1でL0が書かれているとする。
それぞれを処理するインタプリタがint2/1、int1/0であるとすると、図 10の左のようにインタプリタのオーバーヘッドが累積する。
ここでmixを利用すると
out = [[int1/0]]L0 [int2/1, p2, in]
から
int2/0 = [[mix]]L0 [int1/0, int2/1]
となりさらに
comp2/0 = [[cogen]] int2/0
が得られる。これによってオーバーヘッドが削減できる。
コンパイラを作りやすくするためにインタプリタやプログラミング言語の仕様から自動的に正しいコンパイラを作りたい。
(指定されたソース言語からターゲット言語への変換)
[Mauses 1979], [Paulson 1984]
<研究が進展中。>
実行可能な仕様の効率のよい実装(コンパイラやパーサの生成も含まれる)は最も大きな目的。
ここまでに出てきたintやparserを仕様の実行に利用すればよいと自然に考えることが出来る。
[[spec-exec]]L [spec, in1, …, inn] = output
しかし、specを記述しているSと実装言語のLが違うので、そう簡単ではない。
<大きな成果が期待されている。>
部分評価は万能薬ではない。
特殊化は高度な最適化に類似
例: べき乗の例でxが分かっていてもさして高速化の足しにはならない。
例: インタプリタの特殊化で生成されたプログラムはインタプリタの出来に左右される。(例えば動的にサーチして変数名の束縛を行う場合や、動的にソースを生成する場合はターゲットでもそうなる。)
有効なのは:
¨ 時間が掛かる処理
¨ 繰り返し行われる処理
¨ 似たようなパラメタで何度も行われる処理
¨ 構造化され明快に書かれたプログラム(そうでなければ人間だけでなく特殊化プログラムにとっても扱い難い)
¨ 高レベルなアプリケーション志向言語で書かれたプログラム
類似の問題群に対して:
効率のよい(長所)プログラムを沢山書く(短所)
効率は悪いが(短所)汎用でパラメタ化可能なプログラムを1つ書く(長所)
→ 汎用に書いて興味のある目的に特殊化
モジュール化:
界面でオーバーヘッドがある(短所)けれど高度にモジュール化された扱いやすい(長所)プログラム
界面が少なく効率がよい(長所)が一枚岩で扱い難い(短所)プログラム
→ 特殊化によって界面のオーバーヘッドを除去
汎用の正規表現認識プログラムを特定の正規表現に特殊化して速度向上。
[Consel and Dnvy 1989]、[Dnavy 1991]
レイ・トレーシングで特定のシーンに特殊化して速度向上。
[Andersen 1994]、[Mogensen 1986]
問い合わせ言語を特定目的の問い合わせに特殊化してサーチ・プログラムとして利用。さらにそれをプログラム・ジェネレータに入力して問い合わせをサーチ・プログラムに変換するコンパイラを生成
[Safra and Shapiro 1986]
メタ・インタプリタを正当性の検証用に特殊化
[Leusche and De Shreye 1995]
特定のネットワーク・トポロジーに特殊化して学習を高速化
[Jacobsen 1990]
対話的に利用される表計算プログラムを特定目的に特殊化
[Appel 1988]
特殊化時に計算するか実行時に計算するかの認識・峻別が重要。
経験的には:
特にインタプリタ型言語の定義ではBinding-time analysisで静的/動的引数をよく区別でき、停止性を確立するのも容易。とはいえ停止性を得るためにはいくらかインタプリタの変更が必要。
合同性はほぼ自動化されているが停止性の保証では保守的に特殊化するしかない(今後の課題)。
ここ数年で急速に進歩したが、重要な問題が残っており理論と実践は完全には遠い。
初期において印象的な結果はあったが限られた言語にしか適用できなかったり、一部の専門家にしか扱えないような難しさがあった(良い特殊化を実現するには詳しいユーザーの助言や目的のプログラムに合わせた評価系自身のチューニングが必要)。
新たな問題を解くためにプログラムを作るには問題を理解する必要があり自動化は難しい。
プログラム変換はこれまで人手で行ってきたことを自動化したもの。
近年の急速な進歩は操作的意味論に関する理解が進んだことによっている。
一般化や展開に際してどの変数が動的でどの変数が静的であるかを訊ねるようであってはいけない。(現状では幾つかのシステムで、巨大すぎるあるいは無限の出力を止めるために必要)
ユーザーは特殊化に由来するような論理の理解や特殊化の働き方の理解を強制されるべきでない。
専門家でない人間が利用することを考えてシステムやデバッグ機能はプログラムについてbinding-time separationした結果についてをフィードバックすべき。
部分計算の利用はYaccのようなパーサ・ジェネレータの利用にしばしば喩えられる。
l
忠実性:
正しい文法→[パーサ・ジェネレータ]→正しい文を正しく解析して解析木を作成し、正しくない文を検出するパーサ
正しいプログラム→[特殊化系]→正しい動作をする特殊化済プログラム
l
注力する部分のズレ:
文法定義時は生成される文に興味:パーサ・ジェネレータ利用時はleft-to-right曖昧性について考えさせられる。
汎用プログラム作成時はその動作に興味:部分評価系利用時はbinding-time improovements(どうやったらbinding-time separationがうまく行って高速化できるか)について考えさせられる
自動化の試みの足元(ソフトウェアやハードウェアのアーキテクチャや好み)は絶えず変化していて大変困難を伴う。(例えば昨日まで有効だった最適化技法は今日では邪魔なだけかもしれない。)
しかしこれは自動化を軽視することのいい訳にはならない。
<省略>
部分計算とself-applicationは多くの応用があり、プログラム・ジェネレータの生成(コンパイラ、コンパイラ・ジェネレータ、プログラム変換系)に役立つ。
急速に進歩している部分計算で繰り返し発生する問題が幾つかある。
l 部分計算の停止性
l 入力プログラムに対する特殊化プログラムの意味論的な忠実性(faithfulness)(停止性、バック・トラック、結果の正当性、他)
l 特殊化による高速化度合いの予想困難性
l 高速化のためのプログラム修正の困難性
必要とされていること:
¨ 部分評価系を利用しやすくする
¨ どの程度の高速化が可能なのかを理解する
¨ 特殊化を行う前に高速化の効果とメモリ使用量を予測する
¨ 型付き言語における特殊化を改良する
¨ コードの爆発的増加を(自動的に)回避する
¨ インタプリタで定義されたソース言語向けに、キチンとしたマシン・アーキテクチャを生成する
より詳しくは
[Jones rt al. 1993]と[Ruf 1993]を参照。
結局静的/動的の区別(annotationの付け方)が問題
Binding Analysisについて調べる
型との関連を調べる